問題はこちら（画像をクリックするとPDFファイルで開きます。）
有名な難問であり、多くの上級参考書にも収録されています。
色々な上級テーマが含まれており、一つ一つは難関大を目指すうえで糧となるポイントなのですが、逆に
結局何が大事なのか
を見失う可能性もあります。
この問題を扱うにあたっては
大枠としてのポイント
- 存在命題と全称命題の扱い
処理上のポイント
\(a\) , \(b\) を互いに素な整数としたときの \(ax+by\) の扱い
に絞りたいと思います。
その他、周期性に関する別解なども考えられますが、ポイントを絞ることを優先し、今回は見送ります。
（以下ネタバレ注意）
+ クリック（タップ）して続きを読む 今回の問題の主張を把握します。 何を言っているのかが分からないと手の打ちようがありません。 ひとまず、言われているような図形的イメージを考えてみます。 ひとまず、格子点と直線を描いてみました。 ここから円を「膨らませる」というイメージで \(r\) を考えていきます。 直感的には となります。 逆に \(r\) が小さいときを考えてみます。 極端な話、\(r\) がほとんど \(0\) に近いようなとき、ほとんど円は点に近いような状況です。 つまり、 という可能性があるわけです。 本問は \(r\) が大きいと、円とぶつかるのは当然です。 そこで、\(r\) を小さくしていきます。 ただ、\(r\) を小さくしすぎるとぶつからなくなってしまいます。 さて、小さくできる限界はどこですか？ という問いかけということになります。 \(r\) が大きいとぶつかるのは当然 と言いましたが、その式的根拠を考えていきます。 直線と円が共有点をもつということの翻訳は という２路線ありますが、点と直線の距離公式の活用の方が処理的な負担が少なくなることが多く、こちらで攻めるのが第一感です。 傾きが \(\displaystyle \frac{2}{5}\) の任意の直線を \(2x-5y-k=0\) とし、これとある格子点 \((m \ , \ n)\) との距離 \(d\) について \(d \leq r\) となれば、この直線と\((m \ , \ n)\) を中心とする半径 \(r\) の円が共有点をもちます。 つまり \(\displaystyle \frac{|2m-5n-k|}{\sqrt{2^{2}+(-5)^{2}}} \leq r\) が成り立つときに共有点をもつことになります。 全称命題とは 全称命題 全ての〇〇に対して、＊＊が成り立つ という形の命題です。 それに対して、存在命題とは 存在命題 ＊＊が成り立つような、ある〇が存在する。 という形の命題です。 全称命題は文字通り、「全ての」ですから、イメージとしては あれも、これも、それも \(\cdots\) というイメージです。 存在命題は、「ある」なので 「上手い」〇が存在する（一つでも存在すればよい） というイメージです。 本問において、今の全称命題と存在命題を意識してみると 任意の実数 \(k\) に対して、 \(\displaystyle \frac{|2m-5n-k|}{\sqrt{29}} \leq r\) となるような整数 \(m\) , \(n\) が存在する。 という全称命題と存在命題が混在している形です。 という主張です。 ここで、\(2m-5n\) という形の整数は全ての整数を表し得ます。 この項目についてスポットを当てた話題は 例題はこちら（画像をクリックするとPDFファイルで開きます。） \(a\) , \(b\) , \(c\) を整数として \(ax+by=c\) という形の不定方程式（ディオファントス方程式）の整数解 ... 続きを見る の中で詳しく解説しています。 先ほどの 任意の実数 \(k\) に対して、 \(\displaystyle \frac{|2m-5n-k|}{\sqrt{29}} \leq r\) となるような整数 \(m\) , \(n\) が存在する。 という命題は 任意の実数 \(k\) に対して、 \(\displaystyle \frac{|N-k|}{\sqrt{29}} \leq r\) となるような整数 \(N\) が存在する。 という命題で考えればよいことになります。 ラフな言い方で言えば という先ほどの主張は という主張になるわけです。 分母を払えば 任意の実数 \(k\) に対して、 \(|N-k| \leq \sqrt{29}r\) となるような整数 \(N\) が存在する。 となり、この命題が真となるような \(r\) の最小値を求めればよいことになります。 これについては \(N\) と \(k\) の距離が \(\sqrt{29}r\) 以下 というイメージでとらえます。 \(r\) が大きいと、うまく \(N\) をとれる余地があり、冒頭述べた \(r\) が大きいと円とぶつかるという直感とも一致します。 ここで \(N\) は整数としてうまくもってこれるかどうかを考えるわけです。 これをふまえると ことになります。 つまり、 \(r \geq \displaystyle \frac{\sqrt{29}}{58}\) であれば、題意を満たすことになります。 この流れで言えば、あくまでこれは十分条件で、題意を満たすのであれば \(r \geq \displaystyle \frac{\sqrt{29}}{58}\) となるしかない。（なる必要がある） という必要条件かどうかは別途調べる必要があります。 これについては ということを言うことになるわけです。 つまり、\(r \lt \displaystyle \frac{\sqrt{29}}{58}\) のときには、 なにかやばい \(k\) がいて、どんな整数 \(N\) をもってきても \(|N-k| \gt \sqrt{29}r\) になってしまう。 ということになります。 【解答】ではこれを背理法を用いて記述しました。 全称命題については、特有の考え方をすることも多く、対応を知らなければ白紙になってしまいかねない問題も多々あります。 そんな問題たちに対応することを目的として というシリーズもありますので、よろしければご活用ください。イメージ
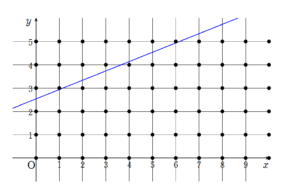
イメージの立式
全称命題と存在命題
\(ax+by\) の形
参考不定方程式の整数解とその発展【ベズーの補題】【2000年度 大阪大学ほか】
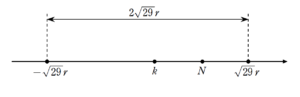
全称命題について
