問題はこちら(画像をクリックするとPDFファイルで開きます。)
文字を含んだ式の大小を比較する問題です。
単純に差を取って解決すれば問題ないのですが、差をとっても埒があかない問題もあるでしょう。
本問は誘導はなく、方針から自力で考える問題です。
もちろん、取っ掛かりとなる部分は無理のない範囲の発想です。
愚直に攻めてもよし、工夫して鮮やかに捌いてもよしという調理の仕方に幅のある問題です。
(以下ネタバレ注意)
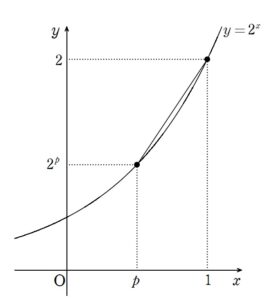
+ クリック(タップ)して続きを読む 今回の2数 \(\displaystyle \frac{2^{a}-2a}{a-1}\) , \(\displaystyle \frac{2^{b}-2b}{b-1}\) は形が揃った2数です。 そこで、これらの2数を \(f(a)\) , \(f(b)\) という形で見立てることを考え \(f(x)=\displaystyle \frac{2^{x}-2x}{x-1}\) (\(0 \lt x \lt 1\)) と設定します。 この関数 \(f(x)\) の振る舞いを調べるために、この後当然微分することになるでしょう。 詳しい計算はここでは割愛しますが、\(f'(x)\) を計算すると \(f'(x)=\displaystyle \frac{2^{x}\{(x-1) \log{2}-1\}+2}{(x-1)^{2}}\) となります。 もちろん、我々の興味は \(f'(x)\) の符号であり、符号に影響を与える分子のみを取り出し \(g(x)=2^{x}\{(x-1) \log{2}-1\}+2\) と設定します。 これも詳しい計算は割愛しますが、 \(g'(x)\) を計算すると \(g'(x)=2^{x}(\log{2})(x-1)\) となり、\(0 \lt x \lt 1\) の範囲では \(g'(x) \lt 0\) となり、\(g(x)\) は単調減少ということになります。 これにより、 \(g(x) \gt g(1)=0\) ということになります。 細かな注意 \(0 \lt x \lt 1\) という範囲なのに \(g(1)\)なんてものを考えていいの? という律儀な人もいるでしょう。 これに対しては という2つの返答が考えられます。 解答では一応後者の立場で解答を作ってあります。 これにより、\(f'(x) \gt 0\) ということが言えるため、\(f(x)\) が単調増加ということが言え、\(0 \lt a \lt b \lt 1\) のとき \(f(a) \lt f(b)\) すなわち \(\displaystyle \frac{2^{a}-2a}{a-1} \lt \displaystyle \frac{2^{b}-2b}{b-1}\) ということが言えます。 今回の2数 \(\displaystyle \frac{2^{a}-2a}{a-1}\) , \(\displaystyle \frac{2^{b}-2b}{b-1}\) は形的に 何かの傾き を彷彿とさせる形をしています。 ただし、このまま見ていても中々埒があきません。 似たような形である \(\displaystyle \frac{2^{p}-2}{p-1}\) であれば、 というように、 というように図形的な意味付けを与えることができます。 そこで、今回考える形の \(\displaystyle \frac{2^{x}-2x}{x-1}\) を $$\begin{eqnarray} と \(\displaystyle \frac{2^{x}-2}{x-1}\) が登場するように無理やり変形してやると、\(-2\) という部分は根本的に関係がないため、結局は \(\displaystyle \frac{2^{a}-2}{a-1}\) と \(\displaystyle \frac{2^{b}-2}{b-1}\) という2数の大小比較で事足りることになります。 解答では、これを逆算的に(天下り的に)記述していけばよいでしょう。路線1:愚直に攻める
路線2:視覚化
\displaystyle \frac{2^{x}-2x}{x-1} &=& \displaystyle \frac{2^{x}-2-2x+2}{x-1} \\
&=& \displaystyle \frac{2^{x}-2-2(x-1)}{x-1}\\
&=& \displaystyle \frac{2^{x}-2}{x-1}-2
\end{eqnarray}$$

