問題はこちら(画像をクリックするとPDFファイルで開きます。)
円周上の正 \(4n\) 角形の頂点を用いて三角形を作るという、素材としてはよくある問題です。
ただ、素材は定番でも中身はマニュアル的態度で倒す態度の問題ではありません。
「結局こうなっていればいい」
ということを見抜く観察力や洞察力を要する問題です。
最後の最後まで気が抜けない要素も含んでおり、試験場では全体のセット次第で撤退するかどうかの判断に迫られる類の問題でしょう。
難易度的には絶妙な難易度です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む イメージとしては という、正方形\(\mathrm{P_{0}}\)\(\mathrm{P}_{n}\)\(\mathrm{P}_{2n}\)\(\mathrm{P}_{3n}\) の一辺の長さが \(\sqrt{2}\) であるイメージが持てれば、即 \(n \leq k \leq 3n\) と片付きます。 結局、 というイメージが大切です。 ひとまず3頂点の1つを \(\mathrm{P_{0}}\) で固定して考えます。 そうなると正方形 \(\mathrm{P_{0}}\)\(\mathrm{P}_{n}\)\(\mathrm{P}_{2n}\)\(\mathrm{P}_{3n}\) によって分けられる4つの弧に注目したくなるでしょう。 今、反時計回りに順に決めていくとして、 とします。 そうなると にくることになります。 つまり、\(l\) の範囲は \(n \leq l \leq 2n\) ということになります。 とします。 \(\mathrm{P}_{l}\mathrm{P}_{m} \geq \sqrt{2}\) を満たすためには先述した ということを意識すれば というイメージをもつことができ、 \(l+n \leq m \leq 3n\) という、\(m\) の範囲を得ることができます。 結局頂点の1つを \(\mathrm{P_{0}}\) としたとき 2点目を \(\mathrm{P}_{l}\) ( \(n \leq l \leq 2n\) ) とすると 3点目の取り方は あり、これを \(l=n\) のとき、\(l=n+1\) のとき、\(\cdots\) と数え上げていけばよく \(\displaystyle \sum_{l=n}^{2n}(2n-l+1)\) とシグマ計算で数えればよいわけです。 これを計算すると、 \(\displaystyle \frac{(n+1)(n+2)}{2}\) を得ます。 頂点の1つを \(\mathrm{P_{1}}\) , \(\mathrm{P_{2}}\) , \(\cdots\) \(\mathrm{P}_{4n-1}\) としたときも同様なので \(\displaystyle \frac{(n+1)(n+2)}{2} \times 4n=2n(n+1)(n+2)\) 【通り】 と数えていきます。 うっかり、このまま \(2n(n+1)(n+2)\) 通り という結論にしてしまいかねませんが、これだと最後の最後でオジャンです。 例えば というパターンを別々のものとしてカウントしています。 しかし、この3パターンの結果出来上がる三角形は同じものです。 このように、一つの三角形に対して3倍多くカウントされているわけです。 したがって求める \(g(n)\) というのは \(g(n)=\displaystyle \frac{2n(n+1)(n+2)}{3}\) ということになります。 「例えば」というモデルケースを考えると、要領がつかみやすいと思います。 いきなりで混乱しそうであれば、一度具体的なモデルケースを何個か考えて見て、 「他も同じ要領じゃね?」 という気持ちになれれば半分はもらったようなものでしょう。 円周上の点によってできる三角形に関する問題としてよくある定番は 鋭角三角形や鈍角三角形を数えさせる という問題です。 この定番寄りの話題については 問題はこちら(画像をクリックするとPDFファイルで開きます。) この手の問題は多くの問題集などにも収録されており、一度は経験したことのある人も多いでしょう。 また、正六角形や正八角形など ... 続きを見る で扱っていますので、必要に応じてご活用ください。(1) について
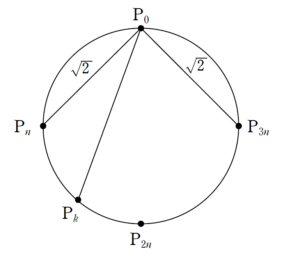
(2) について
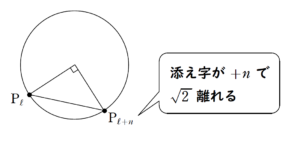
1点目の固定
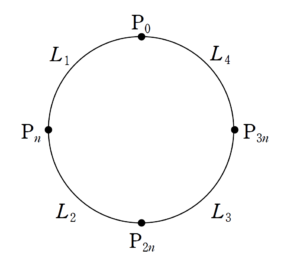
2点目の固定

3点目の範囲
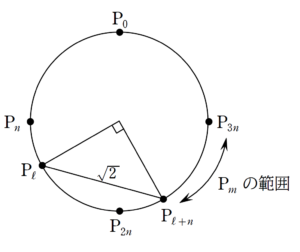
まとめると
重複発生
まとめ

参考正n角形の頂点によって作る三角形【2017年度 同志社大学】

