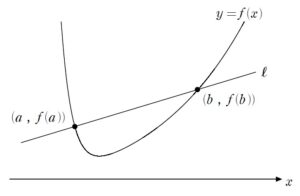
状況の把握
ひとまず状況を把握するために、軽く図示してみると

というイメージです。
「\(f(x)\) が下に凸である」という条件から、区間 \(a \leq x \leq b\) においては、直線 \(l\) は \(y=f(x)\) の上側に存在します。
曲線上の任意の2点をとって結んだ線分より「下に膨らんでいる」とき、その曲線は下に凸と呼ばれます。
直線の方程式の立式
面積計算するにあたり、直線 \(l\) の方程式を求めにいきます。
直線 \(l\) は
- 傾き:\(\displaystyle \frac{f(b)-f(a)}{b-a}\)
- 通過点:\((a \ , \ f(a))\)
であることから
\(y=\displaystyle \frac{f(b)-f(a)}{b-a}(x-a)+f(a)\)
ということになります。
面積の立式
今回考える部分の面積 \(S\) は
\(S=\displaystyle \int_{a}^{b}\{\displaystyle \frac{f(b)-f(a)}{b-a}(x-a)+f(a)-f(x)\} dx\)
となります。
この時点で結構いかつい形をしていますが、結局は
\(\displaystyle \int_{a}^{b}\{(定数)(x-a)+(定数)-f(x)\}dx\)
という形なので、「どうやって積分するの?」という部分では困らないはずです。
見た目のいかつさにビビらずにこの積分計算を進めていくと、約分などで消える部分は消え、思っているよりもメチャクチャな式にはなりません。
詳しい計算過程は【解答】で確認してください。
結果は
\(S=\displaystyle \frac{1}{2}(b-a)\{f(a)+f(b)\}-\displaystyle \int_{a}^{b}f(x) dx\)
となります。
\(f(x)\) が具体的に与えられていない以上、これをほぐすのは限界です。
逆から攻める
今回の問題は幸いなことに「証明形式」での出題です。
そこで、示すべき結論の右辺
\(\displaystyle \frac{1}{2} \displaystyle \int_{a}^{b}(x-a)(b-x)f''(x) dx\)
を変形して、先ほどの
\(\displaystyle \frac{1}{2}(b-a)\{f(a)+f(b)\}-\displaystyle \int_{a}^{b}f(x) dx\)
となることを目指します。
部分積分のインスピレーション
そうなると、\(\displaystyle \int_{a}^{b}〇f''dx\) という形から、\(\displaystyle \int_{a}^{b}f(x)dx\) の形を登場させる必要があり、
部分積分
が頭をよぎると思います。
部分積分は
\(( \ \ \ \ )'\) のつけかえ
という側面をもつ積分方法だからです。
ここまでできれば、あとはゴリゴリ進めるのみです。
試験場での危険性
今回、\(f(x)\) が具体的に与えられているわけではありません。
ただ、皆さんがよく知っているように
放物線と直線で囲まれた部分の面積
というのは、工夫の余地がある話題です。
先ほど出した、直線 \(l\) の式が
\(y=\displaystyle \frac{f(b)-f(a)}{b-a}(x-a)+f(a)\)
と見た目だけで言えば強面であることも相まって
「何かうまい方法があるのか?」
と疑心暗鬼になりやすく、特に試験場ではエレガントに解くことに固執しすぎると、大火傷につながりかねません。
- 多少泥臭くても押し切れるのであれば押し切る
- 手が止まってしまったら、ひとまず他の問題にうつる
という現場での的確な判断をする冷静さも大切です。
(分かってるよと思っていてもできないんですわ、これが)
解答はコチラ