ルーローの三角形【頂点の軌跡】

2022年10月17日

ルーローの三角形と呼ばれる有名図形を扱った問題です。

出典は1987年度の某全国模試です。

本問のオチは原点にあるルーローの三角形の一頂点の軌跡を捉え、その曲線の長さを求めるという問題です。

頭の中でどのような動きをするのかを追っていく必要があり、動的処理から逃げることはできません。

ロータリーエンジンの原理にも使われていたり、パナソニックのルーロという掃除機もこのルーローの三角形が元となっているなど、実用的にも色々応用されています。

（以下ネタバレ注意）

+ クリック（タップ）して続きを読む

(1) について

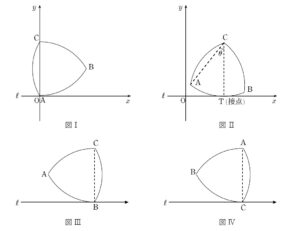
図Ⅰから図Ⅲに至るまでの途中経過が図Ⅱです。

図Ⅱの一般論において

\(\mathrm{CT}=a (一定値)\)

であるため、図Ⅰから図Ⅲに至るまでに、点 \(\mathrm{C}\) は直線 \(y=a\) 上を動くことになります。

そうなると、図Ⅲにおける点 \(\mathrm{C}\) の \(x\) 座標、すなわち \(\mathrm{B}\) の座標が分かれば解決です。

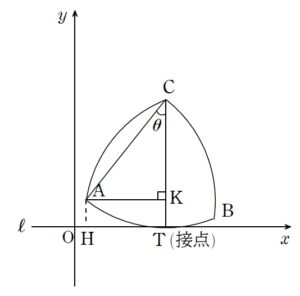
\(\mathrm{A}\)\((X \ , \ Y)\) とおいたとき、\(X\) , \(Y\) を \(a\) , \(\theta\) で表すことを目指します。

と補助線 \(\mathrm{AH}\) , \(\mathrm{AK}\) を引くと分かりやすいでしょう。

として計算すればよいことになります。

いよいよ、この問題のオチである原点に重なっている点 \(\mathrm{A}\) が転がっていったときの軌跡を考える問題です。

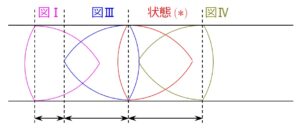
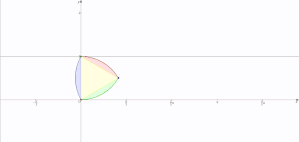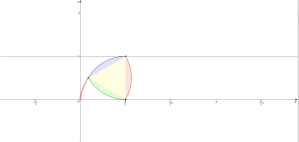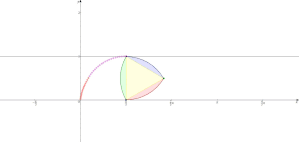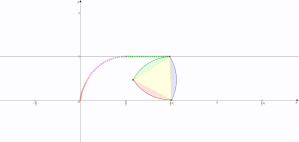
図Ⅱは途中経過なので、図Ⅰ、図Ⅲ、図Ⅳを一つの図の中に書き込むと

となり、大きく分けて３区間で点 \(\mathrm{A}\) の軌跡が表す曲線が変わっていくことになります。

図Ⅰから図Ⅲに至る区間では

サイクロイド

図Ⅲから状態 \((*)\) に至る区間では

円弧

状態 \((*)\) から図Ⅳに至る区間では

直線 \(y=a\)

となります。

今述べたことをアニメーションで表すと

というようになります。

曲線の長さを計算するにあたって、直線部分については (1) の計算結果が使えますし、円弧の部分については \(\displaystyle \frac{\pi}{3}\) 分の回転に伴う円弧の長さです。

ですから、実質積分計算が必要になるのは図Ⅰから図Ⅲに至るまでの区間のサイクロイドの長さの部分です。