問題はこちら(画像をクリックするとPDFファイルで開きます。)
サイコロの目によって決まっていく漸化式から得られる値がある範囲内に収まっている確率を求める問題です。
いかにも何かありそうな設定ですが、切り崩すために必要なものは
10%の工夫と90%の泥臭さ
です。
この問題のオチは「表向き」と「裏向き」の2種類のオチがあります。
どちらも京大が度々用意するオチです。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 今回の \(Y_{n}\) は \(Y_{n}=(サイコロの目)+\displaystyle \frac{1}{Y_{n-1}}\) という形です。 \(\displaystyle \frac{1+\sqrt{3}}{2} \leq Y_{n} \leq 1+\sqrt{3}\) とは という構造です。 この (サイコロの目) は \(3\) , \(4\) , \(5\) , \(6\) だと問答無用でアウト ということになります。 ただ、前後のつながりという点でまだ要領がつかめないでしょうから、ひとまず実験してみます。 \(p_{1}\) とは \(\displaystyle \frac{1+\sqrt{3}}{2} \leq X_{1} \leq 1+\sqrt{3}\) となる確率です。 つまり \(X_{1}=2\) となる確率で、\(p_{1}=\displaystyle \frac{1}{6}\) ということになります。 \(p_{2}\) とは \(\displaystyle \frac{1+\sqrt{3}}{2} \leq X_{2}+\displaystyle \frac{1}{X_{1}} \leq 1+\sqrt{3}\) となる確率です。 ここで 「ん?メンドクセ」 と思います。 \(X_{2}\) は上述したように \(1\) または \(2\) である必要があります。 ただ、\(X_{1}\) については逆数をとる関係で、\(3\) , \(4\) , \(5\) , \(6\) の目が出ても問題ないわけです。 つまり、\(Y_{2}\) が題意の区間に収まっているためには ということが言えるわけです。 この結果は拡張して考えることができ、\(Y_{n}\) が題意の区間に収まっているためには ということが言えることになります。 漸化式 \(Y_{n}=X_{n}+\displaystyle \frac{1}{Y_{n-1}}\) を見ても ということが言えます。 数直線で言えば ということです。 過去なんて関係ない、今なんだよ という修造の声が聞こえてきます。 だったら というように、 「\(q_{n}\) , \(r_{n}\) という設定もしてしまえ」 というのが自然な発想でしょう。 ただ、難関大受験生と言えども、問題で指定されている以上の設定を自分で行うということができる受験生は決して多くはありません。 京大は問題で指定されている以上の設定を要するというこのオチを好んでいるように思います。 これが冒頭述べた「表向き」のオチです。 問題を解くという観点で見れば、どのような経緯で本問が作られたのかを知らなくても解けるには解けます。 ただ、いかにも何かあり気な数字設定ですから、今回の数字の出どころについて見てみることにします。 与えられた漸化式は \(Y_{n}=X_{n}+\displaystyle \frac{1}{Y_{n-1}}\) \(=X_{n}+\displaystyle \frac{1}{X_{n-1}+\displaystyle \frac{1}{Y_{n-2}}}\) \(=X_{n}+\displaystyle \frac{1}{X_{n-1}+\displaystyle \frac{1}{X_{n-2}+\displaystyle \frac{1}{Y_{n-3}}}}\) というように、番号を下げていくと、連分数展開がインスピレーションされると思います。 そういった意味で今回の2つの値 \(\displaystyle \frac{1+\sqrt{3}}{2}\) と \(1+\sqrt{3}\) を連分数展開してみると今回の問題のカラクリが見えてくると思います。 そのことについては【総括】のあとで軽く触れてありますので、余裕と興味があればご覧ください。 これが冒頭述べた「裏向き」のオチです。 この表向きのオチと裏向きのオチを兼ね備えた問題を京大は2015年度にも出題しています。 問題はこちら(画像をクリックするとPDFファイルで開きます。) \(\displaystyle \frac{1}{2}\) からスタートし、2種類の関数を用いて次々と値を出して数列を作っていくという操 ... 続きを見るこの漸化式の構造
実験してみる
実験の結果から分かったこと
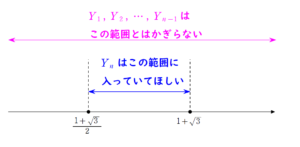
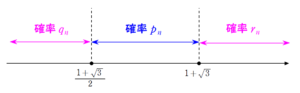
本問の設定の背景

参考漸化式の視覚化【視覚的な意味と操作の意味を考える】【2015年度 京都大学】

