問題はこちら(画像をクリックするとPDFファイルで開きます。)

縦軸回転体の体積をシンプルに問いかけている潔い問題です。
もちろん
単調性のある\(y\) 軸回転体の体積については
\(\displaystyle\int_{a}^{b}\pi x^{2} dy\)
という \(y\) 軸回転体の体積の公式をそのまま使えばいいのですが、単調性のある曲線ばかりではなく、「くり抜き」が必要な問題も多く出題されています。
手際よく処理していくことが求められます。
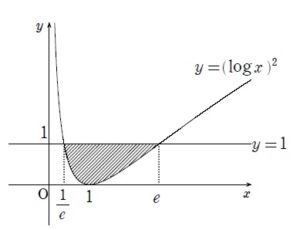
さすがに \((\log x)^{2}=2\log x\) というとんでもない誤答をやらかす方は難関大志望者にはいないと思いますが、一応注意を促しておきます。
(『なめんじゃねぇよ』と思ってください。)
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
まずは微分して増減表を書き、グラフを図示し状況を把握します。
今回は

という状況ですから、くり抜きが必要になります。
くり抜きが必要な \(y\) 軸回転体の体積の王道的な倒し方は
という態度が有効、かつ分かりやすい方針です。
今回は \(y=(\log{x})^{2}\) というある意味分かりやすい関数として与えられていますが、これを敢えて
\begin{eqnarray}
\left\{
\begin{array}{l}
x= t \\
y = (\log t)^{2}
\end{array}
\right.
\end{eqnarray}
とパラメータ表示して処理していきます。
パラメータ表示では、パラメータ ( ここでは \(t\) ) の範囲を簡単に調節でき、くり抜くために曲線を2つに分ける必要があるという要求に応えてくれます。
実際に【解答】を見た方が、パラメータ表示で倒す威力が伝わると思います。
また、縦軸回転体の話題では
「バームクーヘン分割」
も有名でしょう。
これについては【解答】のあとに、触れておきましたので、詳しくはそちらをご覧ください。
バームクーヘン分割については、あくまで検算用にしたほうがよいでしょう。
本問レベル(くり抜きの処理が苦ではないレベル)であれば、王道的にパラメータ表示で倒してほしいです。
あまりにもくり抜きが大変なものであれば、減点覚悟で使うぐらいかなと思います。
なお、斜軸回転体の体積という、これまたテーマ性をもった話題もあるので、そちらもよろしければやってみてください。
-

-
斜軸回転体の体積【傘型積分】【コーン積分】【2006年度 横浜国立大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 斜軸回転体の体積というテーマ性のある話題です。 通常の \(x\) 軸回転体、\(y\) 軸回転体に加え、マスターしておき ...
続きを見る
解答はコチラ