問題はこちら(画像をクリックするとPDFファイルで開きます。)
壺から壺へ球を移動させていき、最後の壺から白球が取り出される確率を考えます。
人によっては直感で分かってしまう人もいるかもしれません。
難易度的にはキッチリ差が付くちょうどよい難易度でしょう。
どちらかというと、問題の構造を分析してその場で対応する力を要する問題です。
問題文を見て睨めっこしてしまうタイプの人を弾くフィルターが付いています。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む いきなり、\(n\) 個目の壺にいくのは難しいでしょうから、ひとまずは実験してみて様子を掴んでみることにします。 \(k\) を正の整数として とします。 \(p_{1}\) については迷いなく \(p_{1}=\displaystyle \frac{a}{a+b}\) と即答です。 \(p_{2}\) は というように、 または というように、 という2つの場合があります。 したがって、 $$\begin{eqnarray} となります。 ここまでくると あれ? となるでしょう。 という予測が立ちます。 予測が立てばそれを数学的帰納法で証明します。 この操作は一定のアルゴリズムによるものであることに注目すれば 漸化式の立式 というのも有力な方針の一つです。 この路線については【戦略2】【解2】で触れています。 結局第2の壺以降は、 と、赤球を追加された状態か という白球を追加された状態 のいずれかしかありえません。 ある意味、 というようなことはなく、何番目の壺かによらず、白が取り出される確率は一定であるという本問の結果は納得がいきやすいかもしれません。 本問と似たような話題で「ポリアの壺」という話題があります。 それに比べれば、本問は比較的マイルドな難易度で収まっていると言えましょう。 問題はこちら(画像をクリックするとPDFファイルで開きます。) ポリアの壺と呼ばれる有名問題です。 経験がないと、右往左往することになると思います。 結果自体は分かりやすく、インパクトがあるものですか ... 続きを見る 難関大志望者については一度は本家ポリアの壺も経験しておくとよいでしょう。いきなりが難しければ実験
\(p_{1}\) について
\(p_{2}\) について
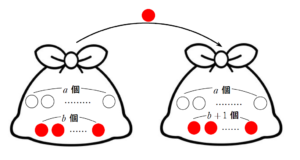
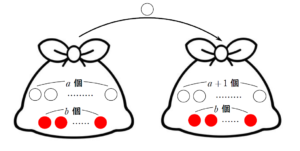
p_{2} &=& \displaystyle \frac{b}{a+b} \cdot \displaystyle \frac{a}{a+b+1}+\displaystyle \frac{a}{a+b} \cdot \displaystyle \frac{a+1}{a+b+1} \\
&=& \displaystyle \frac{a\{b+(a+1)\}}{(a+b)(a+b+1)} \\
&=& \displaystyle \frac{a}{a+b}
\end{eqnarray}$$実験の結果
一定のアルゴリズムに注目すると
振り返ってみると
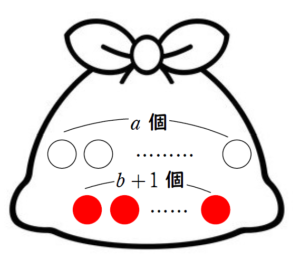
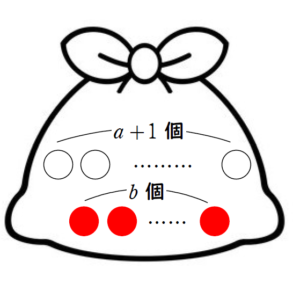

参考ポリアの壺【仮定を味方につける】【2007年度 産業医科大学】

