問題はこちら（画像をクリックするとPDFファイルで開きます。）
最短経路に関する問題は大抵の場合
場合の数・確率
の分野の問題です。
本問は最短経路に関する場合の数ではなく、最短経路を題材として式の扱いや論証力を試す最大最小問題です。
経験と思考力の双方が求められます。
割合的には思考力寄りの問題で、アイデア一つで困難を乗り越える感覚が味わえる好きな問題の一つです。
そのアイデアも突拍子もないものではなく、難関大受験生なら一度はどこかで目にしたことのあるアイデアです。
また、そのアイデアをインスピレーションするための経験の部分についても、これもどこかで目にしたことがあるはずです。
５分１０分考えて答えを見るのはもったいない問題です。
じっくり考えてもらいたい良問ではありますが、時間的にそこまで余裕はないという方も多いでしょう。
最低限志望校の１題あたりにかけられる時間程度は考えてみてほしいと思います。
（以下ネタバレ注意）
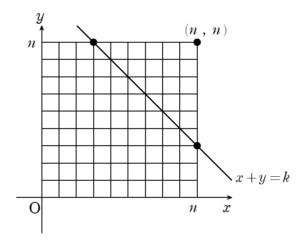
+ クリック（タップ）して続きを読む \(x\) 座標と \(y\) 座標の和が \(k\) という状況、すなわち \((x \ , \ y)\) が、直線 \(x+y=k\) 上 という状況を意味します。 最短経路の問題において というような斜めのラインがあり、 ということが言えます。 最短経路の問題を何題か経験していれば、この発想は一度は目にしたことがあると思います。 先ほどの \((x \ , \ y)\) が、直線 \(x+y=k\) 上 という状況も考えると、ますます斜めラインである直線 \(x+y=k\) に目が行くでしょう。 \(k=0 \ , \ 1 \ , \ 2 \ , \ \cdots \ , \ 2n\) に対して、最短経路 \(\mathrm{P}\) の通る直線 \(x+y=k\) 上の格子点を \((x_{k} \ , \ y_{k})\) とします。 すると、題意の和は \(\displaystyle \sum_{k=0}^{2n}(x_{k}+y_{k})\) です。 もちろん、\((x_{k} \ , \ y_{k})\) は直線 \(x+y=k\) 上の点ですから \(x_{k}+y_{k}=k\) ということが言え、 $$\begin{eqnarray} と、確かに与えられた \(n\) にのみ依存し、経路に依らない一定値となることが言えました。 今度は題意の和は \(\displaystyle \sum_{k=0}^{2n}({x_{k}}^{2}+{y_{k}}^{2})\) です。 もちろん \(x_{k}+y_{k}=k\) と結びつけるために $$\begin{eqnarray} と見たいところです。 これにより、\({x_{k}}^{2}+{y_{k}}^{2}\) が最大のときを考えたければ ということになります。 \(x+y=k\) 上の格子点 \((0 \ , \ k)\) , \((1 \ , \ k-1)\) , \(\cdots\) , \((k-1 \ , \ 1)\) , \((k \ , \ 0)\) に対し、\(x\) 座標と \(y\) 座標の積の最小値は \(0\) ということは感覚的に分かります。 つまり、正方形の周上を通って \((n \ , \ n)\) まで行く経路が求めるものなのかという予想は立ちます。 ただ、\(k=n+1 \ , \ n+2 \ , \ \cdots \ , \ 2n\) のときは というように、 \((0 \ , \ k)\) , \((k \ , \ 0)\) が \(x+y=k\) 上に入ってきません。 このあたりでケチをつけられないようにどのように乗り越えるかという部分が頭を使う所でしょう。 ここから先は思考力の範疇です。 \(x_{k}+y_{k}=k\) という関係式を活かそうということを考えてみましょう。発想の方向性
(1) について
\displaystyle \sum_{k=0}^{2n}(x_{k}+y_{k})&=& \displaystyle \sum_{k=0}^{2n}k \\
&=& \displaystyle \frac{2n(2n+1)}{2}\\
&=&n(2n+1)
\end{eqnarray}$$(2) について
{x_{k}}^{2}+{y_{k}}^{2}&=& (x_{k}+y_{k})^{2}-2x_{k}y_{k} \\
&=& k^{2}-2x_{k}y_{k}
\end{eqnarray}$$
