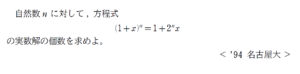問題はこちら(画像をクリックするとPDFファイルで開きます。)
方程式の実数解の個数を数えるというテーマとしてはよくある話題です。
ただなまじ色々見える分、方針決定が難しく、押し通すにしてもそれなりに腕力が必要なので、各方針の引き際を見極めるのが難しいと思います。
試験場ではこういった
色々見えるものがあり、うまくやろうと試みたが結局うまくいかず、愚直にゴリゴリ進めるのが最善だった
という類の問題が厄介です。
特に本問は「作為めいた匂いのする設定」が見た目から漂ってきます。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 例えば など、策に拘りたくなるような見た目です。 自分が解いたときは最初策に拘って \(n\) 乗が鬱陶しいから、\(1+x=t\) と置きなおしてしまえ と考えました。 そうすると、与えられた方程式は \(t^{n}=1+2^{n}(t-1)\) となります。 ここで、思ったのが 最初の方程式は \(x=0\) を解にもつ。 ということで、 \(t^{n}-2^{n}t+2^{n}-1=0\) の左辺が \(t-1\) という因数をもつということで因数分解してみようとしました。 \((t^{n}-1)-2^{n}(t-1)=0\) \((t-1)(t^{n-1}+t^{n-2}+\cdots+t+1)-2^{n}(t-1)=0\) \((t-1)\{(t^{n-1}+t^{n-2}+\cdots+t+1)-2^{n}\}=0\) と確かに目論見通り因数分解できましたが、 \(\{(t^{n-1}+t^{n-2}+\cdots+t+1)-2^{n}\}=0\) をどう捌こうかということで唸りました。 \(t^{n-1}+t^{n-2}+\cdots+t-(2^{n}-1)=0\) \(t^{n-1}+t^{n-2}+\cdots+t-(2-1)(2^{n-1}+2^{n-2}+\cdots+2+1)=0\) \((t^{n-1}-2^{n-1})+(t^{n-2}-2^{n-2})+\cdots+(t-2)-1=0\) と足掻いてもみました。 しかし、決定的なものが見えず、因数分解の路線はこの辺りが引き際だと感じました。 ただ、分かったことは \((t^{n-1}-2^{n-1})+(t^{n-2}-2^{n-2})+\cdots+(t-2)-1=0\) の左辺は \(t=2\) をぶち込むと \(-1\) という値になるわけで、元々の \(t^{n}-2^{n}t+2^{n}-1=0\) という方程式を視覚化する際の、\(y=t^{n}-2^{n}t+2^{n}-1\) が \((2 \ , \ -1)\) を必ず通るということは分かりました。 この事実を活かす路線は、視覚化という言葉を使っていることから分かる通り、グラフを考える「微分法路線」です。 結局は微分法でゴリゴリする路線からは逃れられなかったわけです。 もうここからは割り切ってゴリゴリすることにしました。 ただ、\(=0\) を相手にする前に 左辺と右辺を組み替えて考えやすいようにできないか ということを考えます。 そうなると、元々最初に \(1+x=t\) と置き換えたときに現れる \(t^{n}=1+2^{n}(t-1)\) の方程式で考えるのがよいかなと思いました。 この形で見ることで上述した \(y=t^{n}-2^{n}t+2^{n}-1\) が \((2 \ , \ -1)\) を必ず通る という事実を活かすということは捨てることになります。 しかし、左辺の \(n\) 次関数は偶奇の場合分けこそ必要ですが、振る舞い自体は単純です。 右辺も敢えてこの形で見ることで、\((1 \ , \ 1)\) を必ず通ることが分かりやすいです。 そうなると、気になるのは \(y=t^{n}\) の\((1 \ , \ 1)\) における接線の傾きです。 微分して接線の傾きを調べると \(n\) ということが分かります。 したがって、 \(n\) と \(2^{n}\) の大小が気になりますが、 \(2^{n} \gt n\) であることは即分かるでしょう。 ①:数学的帰納法 ②:二項定理のケツカット です。 数学的帰納法でもよいですが、②のやり方も汎用性があるのでマスターしましょう。 \((1+1)^{n}={}_n \mathrm{ C }_0+{}_n \mathrm{ C }_1+{}_n \mathrm{ C }_2+\cdots+{}_n \mathrm{ C }_{n-1}+{}_n \mathrm{ C }_n\) なので、 \(2^{n} \gt {}_n \mathrm{ C }_1=n\) となります。 ここでは \({}_n \mathrm{ C }_2\) 以降に加え、 \({}_n \mathrm{ C }_0\) もカットしてしまいました。 このあたりの話題で有名なのは ベルヌーイの不等式 \(x \geq 0\) , \(n\) は正の整数とするとき \((1+x)^{n} \geq 1+nx\) という不等式です。 条件の意味
\(x \geq 0\) というのは「カットするものが \(0\) 以上」 ということを保証するための条件です。 自分がグダグダと考えた方針は【解 2】としました。 多くの人は置き換えることなく処理するであろうことと、\(=0\) を相手にするであろうことを考えて、その路線でゴリゴリやっていく方針を【解 1】としました。 その際、解き進める中で という場合分けの必要性に迫られるかと思います。パッと見で気づくこと
だったら、この \(t\) の \(n\) 次方程式は \(t=1\) を解にもつはず。ただでは転ばない姿勢
裏付ける方法
まとめ