問題はこちら(画像をクリックするとPDFファイルで開きます。)

順列に関する問題で、数が5個しかないので全部は大変にしても部分的にゴリゴリ押し通していけばできなくはありません。
最後にモノを言うのは基礎の運用ですが、
何を求めればよいのか
を要約する「咀嚼力」が求められます。
「何を求めればよいか」に辿り着けるからこそ、次の「どう計算すればよいか」に繋がってきます。
場合の数や確率分野である程度のところで頭打ちになっていて、そこからのブレイクスルーを起こすためには、まさにその部分が必要でしょう。
本問は「この問題の類題を期待する」という類の問題ではありませんが、上述の力を養うという点で演習価値のあるいい題材です。
そのためには解答を見る前に考えることを厭わないでください。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
(1) について
\(M=20\) について
\(M=20\) となる場合は分かりやすく、
- \(4\) , \(5\) という上位2数が隣り合う
という並びを考えればよいわけです。
「隣り合う並び」を実現させるための常套手段は
- 一旦紐で縛って並び替え、その後に紐を外してその中で並べ替える
という態度です。
\(M=15\) について
\(M=15\) とは
- \(3\) と \(5\) が隣りあうが、\(4\) と \(5\) は隣り合わない
という並びのときです。
もっと言えば
- \(3\) と \(5\) が隣り合う並べ方から、\(4\) と \(5\) が隣り合うものを除けばよい
ということになります。
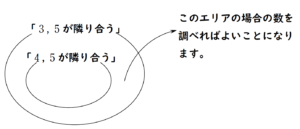
イメージで言えば

このようなベン図のイメージがもてればよいでしょう。
- \(3\) , \(5\) が隣り合う
- \(4\) , \(5\) が隣り合う
という両方を満たす場合、\(5\) の両隣が \(3\) , \(4\) ということになります。
つまり
- \(3\) , \(5\) , \(4\)
- \(4\) , \(5\) , \(3\)
という並びを含むものを考えることになります。
(2) について
\(M=12\) について
次の候補は \(M=12\) です。
これについては
- \(3\) , \(4\) が隣り合うけど、\(M=15\) , \(M=20\) とはならない
ということです。
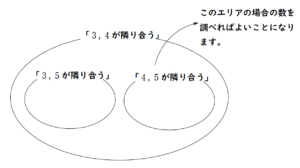
これもベン図のイメージで言えば

このようなイメージをもつことができれば、事故ることはありません。
ちなみに
- \(3\) , \(5\) が隣り合う
- \(4\) , \(5\) が隣り合う
という両者は同時には起こりません。
もし同時に起こるとすると、
- \(3\) , \(5\) , \(4\)
- \(4\) , \(5\) , \(3\)
という並びのように、\(5\) の両隣が \(3\) , \(4\) ということになってしまい、
\(3\) , \(4\) が隣り合うという前提に反する
ということになってしまうからです。
計算の要領自体は (1) での計算と同様の要領で計算できると思います。
\(M\) の候補について
今回は \(M\) のとり得る値を「全て」求めなければなりません。
つまり、「\(M\) はこの値にはならない」ということも含めて論証する必要があるわけです。
ここまでの話で、\(M=20\) , \(M=15\) , \(M=12\) と大きい方から考えてきましたが、これ以外の値になる可能性を検討してみます。
\(M=20\) , \(M=15\) , \(M=12\) とならないとき、
\(3\) , \(4\) , \(5\) はどの2つも隣り合わない
ということになります。
隣り合わない並びを実現させるための常套手段は
という2路線があります。
今回は5個という限られた個数の中で、3個のどれも隣り合わないというかなり限定的なシチュエーションです。
どちらの態度をとっても行き着く先は
\((a_{1} \ , \ a_{2} \ , \ a_{3} \ , \ a_{4} \ , \ a_{5})=(〇 \ , \ □ \ , \ 〇 \ , \ □ \ , \ 〇)\)
- \(〇\) に \(3\) , \(4\) , \(5\) が入る
- \(□\) に \(1\) , \(2\) が入る
という形です。
ここからは洞察力の問題ですが
- \(2\) はどう頑張っても \(4\) , \(5\) のどちらか一方とは隣り合ってしまう
ということが言えます。
つまり、\(M \geq 8\) が確定するわけです。
\(M=9\) , \(M=11\) はあり得ませんから、考えられる可能性としては
\(M=8\) , \(M=10\)
という可能性しかあり得ないことになります。
ここまでくると、ほとんど「形」が決まってきますので、愚直に数え上げてもタカがしれています。
解答はコチラ