直線の通過領域、線分の通過領域【2009年度横浜国立大学】

難関大頻出の話題である「通過領域」の問題の中でも、一番シンプルな「直線の通過領域」について考えます。

さらに、その延長にある「線分の通過領域」についても扱います。

なお、通過領域に関する根本的な考え方については

: 参考逆像法　第３講【通過領域への応用】

問題はこちら（画像をクリックするとPDFファイルで開きます。）逆像法シリーズ第３講は通過領域という難関大入試でも頻出の話題について扱います。このシリーズの一覧はこちら &nbsp ...

続きを見る

で扱っていますので、考え方の根っこについて押さえたい人はそちらを参考にしてください。

本問は逆像法のココロはおさえた上で、線分の通過領域というワンパンチあるテーマを考えるということで、「実践演習」の方で扱います。

（以下ネタバレ注意）

+ クリック（タップ）して続きを読む

直線の通過領域は逆像法が有力候補

今回の直線 \(PQ\) の式は

\(y=(2t+1)x-t^{2}-t\)

です。

題意の通過領域を \(D\) として、

\((X \ , \ Y)\) って \(D\) に入る？

入れるとしたらどんな \((X \ , \ Y)\)？

という逆像法の考えをします。

そうなると、\(Y=(2t+1)X-t^{2}-t\) , すなわち

\(t^{2}-(2X-1)t+Y-X=0\) \(\cdots\) (*)

を満たす実数 \(t\) が存在するかどうかということになります。

(1) は \(t\) が全実数を動くときの通過領域なので、逆像法的には

とにかく \(t\) が実数として存在してくれていればよい

ということです。

よって (*) が実数解をもてばそれでよく、判別式で解決します。

単純に、

(*) が \(-1 \leq t \leq 0\) の範囲に実数解を少なくとも１つもてばよい

だけではいけません。

これは \(-1 \leq t \leq 0\) の範囲で \(t\) を動かしたときの「直線 \(PQ\)」の通過領域ということしか翻訳できていません。

線分の通過領域は、直線の通過領域の部分的なものであるということを考えて、

一旦 \(-1 \leq t \leq 0\) の範囲で \(t\) を動かしたときの「直線 \(PQ\)」の通過領域を捉えて、そのうちのどの部分かを考える作戦でいきます。

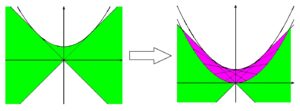
そう考えると、今回の線分\(PQ\) の作り方から、求める通過領域は \(y \geq x^{2}\) の領域に存在するわけなので、

のように直線 \(PQ\) の通過領域を

\(y=x^{2}\) という放物線で「カット」してやる

というように話を進めていければオーケーです。