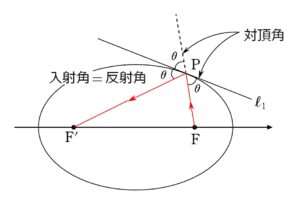
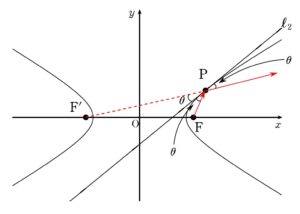
本問の流れとしては
step
1焦点が共通であることを翻訳する
楕円 \(C_{1}\) の焦点 \((\sqrt{\alpha^{2}-\beta^{2}} \ , \ 0)\) と、双曲線 \(C_{2}\) の焦点 \((\sqrt{a^{2}+b^{2}} \ , \ 0)\) が一致することから、
\(\sqrt{\alpha^{2}-\beta^{2}}=\sqrt{a^{2}+b^{2}}\)
すなわち
\(\alpha^{2}-\beta^{2}=a^{2}+b^{2}\)
を得ます。
step
2交点を\(P(p \ , \ q)\) とおき、接線の式を立てる
楕円 \(C_{1}\) と 双曲線 \(C_{2}\) の交点を \(P\) として、先に文字で \((p \ , \ q)\) などとおきます。
これにより、P における \(l_{1}\) , \(l_{2}\) の接線の式はそれぞれ
$$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{px}{\alpha^{2}}+\displaystyle \frac{qy}{\beta^{2}} = 1 \\
\displaystyle \frac{px}{a^{2}}-\displaystyle \frac{qy}{b^{2}} = 1
\end{array}
\right.
\end{eqnarray}$$
ということになります。
step
3\(l_{1}\) , \(l_{2}\) の傾きを出す
今回、楕円 \(C_{1}\) と 双曲線 \(C_{2}\) の交点は座標軸上にはありませんから、\(l_{1}\) , \(l_{2}\) の接線には傾きがあります。
その傾きをそれぞれ \(m_{1}\) , \(m_{2}\) とすると
\(m_{1}=-\displaystyle \frac{\beta^{2}p}{\alpha^{2}q}\) , \(m_{2}=\displaystyle \frac{b^{2}p}{a^{2}q}\)
となり、
\(m_{1}m_{2}=-\displaystyle \frac{p^{2}}{q^{2}}(\displaystyle \frac{b\beta}{a\alpha})^{2}\)
を得ることになります。
step
4交点 \(P(p \ , \ q)\) が満たすべき条件を整理する
\(p\) , \(q\) は
$$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{p^{2}}{\alpha^{2}}+\displaystyle \frac{q^{2}}{\beta^{2}} = 1 \\
\displaystyle \frac{p^{2}}{a^{2}}-\displaystyle \frac{q^{2}}{b^{2}} = 1
\end{array}
\right.
\end{eqnarray}$$
を満たしています。
Step 3 で得た形から \(p^{2}\) , \(q^{2}\) についての連立方程式と見たくなります。
よって、\(p^{2}\) , \(q^{2}\) についての連立方程式として解くと
\(p^{2}=\displaystyle \frac{\alpha^{2}a^{2}(\beta^{2}+b^{2})}{\beta^{2}a^{2}+\alpha^{2}b^{2}}\) , \(q^{2}=\displaystyle \frac{\beta^{2}b^{2}(\alpha^{2}-a^{2})}{\beta^{2}a^{2}+\alpha^{2}b^{2}}\)
ということになります。
比をとってみると、消える部分は消えますし、Step 1 で得た条件式は
\(\alpha^{2}-a^{2}=\beta^{2}+b^{2}\)
の形で使えばよいことが分かります。
全体的に
目標は2つの接線が直交するという「直交条件を示す」という分かりやすい目標であるため、やるべきことが全く見えないということはないと思います。
ただ、計算量は多く、計算のスジが悪いとグチャグチャになりかねません。
使ってよい手持ちの条件と、条件の翻訳で得られた形を観察して、ある程度の見通しを持ちながら計算を進める必要があるでしょう。
試験場で初見で出くわした場合、なおさら平常心を奪われると思います。
解答はコチラ