問題はこちら(画像をクリックするとPDFファイルで開きます。)
最大公約数と最小公倍数に関する不定方程式を解く問題です。
整数問題に対する基本的な手法を確認するとともに、最大公約数、最小公倍数に関する基本的な関係をしっかりと確認しましょう。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む ひとまず \((L+G)(L-G)=2^{3} \cdot 3^{2}\) と因数分解し、積の形を作って 約数を拾う という整数問題の基本を狙っていくのが自然でしょう。 手際が多少悪くなったとしても \(L\) , \(G\) は求まる というのを心の支えとしたいところです。 \(L+G \gt 0\) ですから、 (負の整数) \(\times\) (負の整数) という形は考えなくてもよくなります。 \(L+G \gt L-G \gt 0\) ですから、例えば \(8 \times 9\) , \(9 \times 8\) のうち、片方のみを考えればよいことになり、さらに省エネ出来ます。 以上から という組が出来上がります。 ここからしらみつぶしに連立方程式を解いて \(L\) , \(G\) を出してもたかが知れていますが、もう少し省エネしてみたいと思います。 \((L+G)+(L-G)=2L\) ということで、 和が偶数 となっています。 これにより \(L+G\) , \(L-G\) の偶奇が一致する ということが言えます。 ということで、先ほどの からさらに候補が削れて という3組となります。 ここから、 \((L \ , \ G)=(19 \ , \ 17) \ , \ (11 \ , \ 7) \ , \ (9 \ , \ 3)\) が得られることになります。 \(a\) , \(b\) の最大公約数を \(G\) とすると、互いに素な正の整数 \(\alpha\) , \(\beta\) を用いて $$\begin{eqnarray} と表せます。 このとき、\(a\) , \(b\) の最小公倍数 \(L\) は \(L=G \alpha \beta\) と表せます。 \(a\) の倍数は \(G \alpha \times (整数)\) という形で書けます。 \(b\) の倍数は \(G \beta \times (整数)\) という形で書けます。 よって、\(a\) , \(b\) の公倍数は \(G \alpha \beta \times (整数)\) という形で書けます。 この形で書ける最小の正整数が最小公倍数 \(L\) であるため \(L=G \alpha \beta\) ということになるわけです。 \(L=G \alpha \beta\) の両辺に \(G\) をかけると \(GL=G \alpha \cdot G \beta\) ということになり、 \(GL=ab\) という関係式が成り立ちます。 先ほど \((L \ , \ G)=(19 \ , \ 17) \ , \ (11 \ , \ 7) \ , \ (9 \ , \ 3)\) と、\(L\) , \(G\) の値の組が得られましたが、 \(L=G \alpha \beta\) という関係式から \(L\) は \(G\) の倍数となっている ということが言えます。 このことから \((L \ , \ G)=(9 \ , \ 3)\) という組しか残らないことになります。 これより \(9=3 \alpha \beta\) すなわち \(\alpha \beta=3\) ということになり、 \((\alpha \ , \ \beta)=(1 \ , \ 3) \ , \ (3 \ , \ 1)\) を得て、 $$\begin{eqnarray} に代入すれば \((a \ , \ b)=(3 \ , \ 9) \ , \ (9 \ , \ 3)\) と得られて解決します。 $$\begin{eqnarray} とおいたときに \(L=G \alpha \beta\) となりますが、これを与えられた関係式 \(L^{2}-G^{2}=72\) に代入すると \({\alpha}^{2}{\beta}^{2}G^{2}-G^{2}=72\) すなわち \(({\alpha}^{2}{\beta}^{2}-1)G^{2}=72\) という関係を得ます。 これも 積の形から約数を拾っていく という基本ですが、 \(G^{2}\) が平方数である ということが強力に候補を絞ってくれます。 \(G^{2}\) は \(72\) の正の約数であると同時に平方数であるという強力な条件によって、色々可能性が削られていきます。 この路線は【解2】で扱っています。最初の心構え
約数を拾う際の省エネ
符号について
大小について
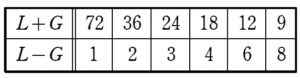
偶奇について

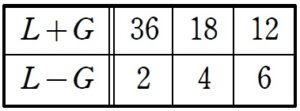
最大公約数と最小公倍数に関する関係
\left\{
\begin{array}{l}
a=G \alpha \\
b=G \beta
\end{array}
\right.
\end{eqnarray}$$理由
補足
本問の続き
\left\{
\begin{array}{l}
a=3 \alpha \\
b=3 \beta
\end{array}
\right.
\end{eqnarray}$$路線その2
\left\{
\begin{array}{l}
a=G \alpha \\
b=G \beta
\end{array}
\right.
\end{eqnarray}$$

