問題はこちら(画像をクリックするとPDFファイルで開きます。)
双曲線とその性質について確認する問題です。
本問は
- 双曲線の焦点についての導出
- 双曲線の幾何的な性質
- 双曲線と直線の連立と、その後の処理
- 双曲線の漸近線
というように、この1問の中でこれだけの各種基本事項を含んでいるコスパの良い標準問題です。
何かいい問題ないかなぁという指導者側からすれば「あ~ざ~す」的問題です。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む 一般に、 双曲線 \(\displaystyle \frac{x^{2}}{a^{2}}-\displaystyle \frac{y^{2}}{b^{2}}=1\) の焦点は \((\pm \sqrt{a^{2}+b^{2}} \ , \ 0)\) で与えられます。 本問は \(x \gt 0\) の範囲にある方の焦点なので、求める焦点の \(x\) 座標は \(\sqrt{2^{2}+1^{2}}=\sqrt{5}\) と即終わります。 今回は、 が \(x \gt 0\) の範囲で異なる2つの共有点をもつような \(k\) の範囲を求めることになります。 式的に言えば、\(y\) を消去した \(\displaystyle \frac{x^{2}}{4}-\{k(x-\sqrt{5})\}^{2}=1\) を整理して出てくる \((4k^{2}-1)x^{2}-8\sqrt{5}k^{2}x+(20k^{2}+4)=0 \ \cdots (*)\) という \(x\) についての方程式が \(x \gt 0\) の範囲で異なる 2 個の実数解をもつための \(k\) の条件を考えることになります。 ここまで翻訳できれば、2次方程式の解について注文が入るという、典型的な 「解の配置問題」 に帰着するわけです。 そうなってくると、そもそも \((*)\) が2次方程式となっている必要がありますから \(k \neq \pm \displaystyle \frac{1}{2}\) である必要があります。 2次方程式だと確定したとき、判別式 \(D\) に対して、\(\displaystyle \frac{D}{4}\) を計算すると \(\displaystyle \frac{D}{4}=4(k^{2}+1)\) と整理でき、\(\displaystyle \frac{D}{4} \gt 0\) と言えます。 つまり、\((*)\) が異なる 2 つの実数解をもつことは保証されているということになります。 あとは、「2つとも正の解」というハードルをクリアーすればよいわけです。 こうなってくると、 を調べることになるでしょう。 詳しい計算については【解答】で確認してください。 \(k \gt \displaystyle \frac{1}{2}\) となれば OK です。 (2) の結論である \(k \gt \displaystyle \frac{1}{2}\) という結果についてです。 一般に 双曲線 \(\displaystyle \frac{x^{2}}{a^{2}}-\displaystyle \frac{y^{2}}{b^{2}}=1\) の漸近線は \(y=\pm \displaystyle \frac{b}{a} x\) です。 ここではすごいラフな説明で済ませます。 双曲線の上半分は \(y=\sqrt{\displaystyle \frac{b^{2}}{a^{2}}x^{2}-b^{2}}\) で与えられます。 \(\displaystyle \lim_{x \to \infty} \sqrt{\displaystyle \frac{b^{2}}{a^{2}}x^{2}-b^{2}}-\displaystyle \frac{b}{a}x\) という遥か彼方での差を計算してみてください。 \(0\) になります。 つまり、遥か彼方では両者はほとんど同じだということを意味するわけです。 もう半分も同じです。 さて、今回の双曲線 \(\displaystyle \frac{x^{2}}{4}-y^{2}=1\) の漸近線は \(y=\pm \displaystyle \frac{1}{2} x\) です。 という漸近線のイメージがあれば、(2) で出てくる \(k \gt \displaystyle \frac{1}{2}\) という結論も納得がいくでしょう。 一般に、 双曲線 \(\displaystyle \frac{x^{2}}{a^{2}}-\displaystyle \frac{y^{2}}{b^{2}}=1 \ \ (a \gt 0 \ , \ b \gt 0)\) の2つの焦点 \(\mathrm{F}\) , \(\mathrm{F'}\) に対し、 \(|\mathrm{FP}-\mathrm{F'P}|=2a\) が成り立ちます。 というより、 2定点 \(\mathrm{F}\) , \(\mathrm{F'}\) に対して \(|\mathrm{FP}-\mathrm{F'P}|=2a\) が成り立つような点 \(\mathrm{P}\) の軌跡のことを双曲線と呼び、その式の形が \(\displaystyle \frac{x^{2}}{a^{2}}-\displaystyle \frac{y^{2}}{b^{2}}=1 \ \ (a \gt 0 \ , \ b \gt 0)\) という形で与えられる。 というのが元々の定義です。 本問においては、与えられた条件を活用しようと思うと という双曲線の幾何的性質を利用したくなるでしょう。 辺々加えると、条件から \(12-(\mathrm{FA}+\mathrm{FB})=8\) すなわち \(\mathrm{FA}+\mathrm{FB}=4\) となり、即 \(\mathrm{AB}=4\) と解決することになります。 このときの \(k\) の値については、\((*)\) の解 \(\alpha\) , \(\beta\) を用いて として、\({\mathrm{AB}}^{2}\) を計算すればよいでしょう。 この計算については、解と係数の関係を用いて進めていく定番の処理です。(1) について:双曲線の焦点の導出
(2) について:双曲線と直線の連立
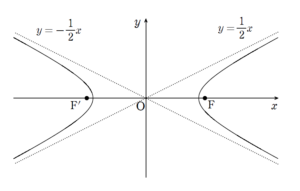
補足:双曲線の漸近線について
(3) について:双曲線の幾何的性質