問題はこちら(画像をクリックするとPDFファイルで開きます。)

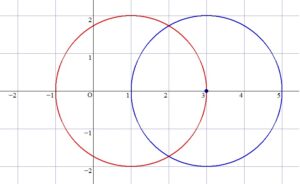
円と円の交点を結ぶ線分の通過領域を求める問題です。
円 \(C\) は固定されていますが、円 \(C'\) の動きは点 \((1 \ , \ 0)\) を通りながら動くというパッと見よく分からない動き方をします。
円 \(C'\) の動きは式的にかろうじて追うことができるでしょう。
その動きに伴う共有弦の動きを細かな部分まで目で追いきるとなると限界があるでしょう。
そのあたりをどのように扱うかは、経験がモノをいいます。
通過領域の根本的な考え方については
-

-
参考逆像法 第3講【通過領域への応用】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 逆像法シリーズ第3講は 通過領域 という難関大入試でも頻出の話題について扱います。 このシリーズの一覧はこちら   ...
続きを見る
で扱っています。
この問題は基本的な考え方をおさえた上での「演習教材」としての位置づけとして扱います。
(以下ネタバレ注意)
+ クリック(タップ)して続きを読む
円 \(C'\) の動き
円 \(C'\) は半径が 2 で一定です。
中心についてはひとまずは \((s \ , \ t)\) とおき、
\((x-s)^{2}+(y-t)^{2}=4\)
と立式します。
これが \(P\) \((1 \ , \ 0)\) を通るので、\((1-s)^{2}+(0-t)^{2}=4\) , すなわち
\((s-1)^{2}+t^{2}=4\)
を得ます。
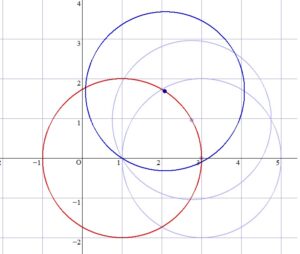
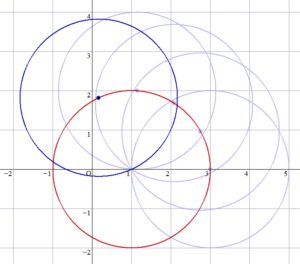
つまり、円 \(C'\) の中心は、中心が \((1 \ , \ 0)\) , 半径 2 の円周上を動きます。



といった感じでしょうか。
とは言え、円 \(C'\) の動きは追えても、それによってできる共有弦の動きを追っていくのは難しいでしょう。
そこで逆像法の出番です。
そのために2円の交点を結ぶ直線の式を捉えます。
2円の交点を結ぶ直線の式は \(\cdots\)
円 \(C\):\(x^{2}+y^{2}=4\) \(\cdots\) ①
円 \(C'\):\((x-s)^{2}+(y-t)^{2}=4\) \(\cdots\) ②
の交点を結ぶ直線の式は①\(-\)②で得られる
\(2sx-s^{2}+2ty-t^{2}=0\) \(\cdots\) ③
として与えられます。
なぜなら ① , ② を満たす \((x \ , \ y)\) (すなわち交点)は ③ を満たしており、
交点が直線③上にある
ということになるからです。
交点同士を結ぶ直線は一意的に定まることを考えれば、直線③が2交点を通る直線ということに他なりません。
線分の通過領域は厄介
今回求めるのは「線分」の通過領域ということで、逆像法を用いたとしても大変です。
本問で求めたい通過領域は
\(x^{2}+y^{2} \leq 4\) という円 \(C\) の内部に存在する
ということになります。
そこで、「一旦「直線」の通過領域を求め、それを円 \(C\) でカット」するという方向性を睨んでいきます。
この後は、
\((X \ , \ Y)\) は通過領域に含まれる?
含まれるとしたらどんな\((X \ , \ Y)\) ?
という逆像法の考え方で仕留めていきます。
場数を踏みたい方は
逆像法による通過領域の考え方を運用していく問題は場数を踏んでおくことも大切です。
場数を踏みたい方は
-

-
直線の通過領域、線分の通過領域【2009年度 横浜国立大学】
問題はこちら(画像をクリックするとPDFファイルで開きます。) 難関大頻出の話題である「通過領域」の問題の中でも、一番シンプルな「直線の通過領域」について考えます。 さらに、その延長にある「線分の通過 ...
続きを見る
も活用してください。
解答はコチラ